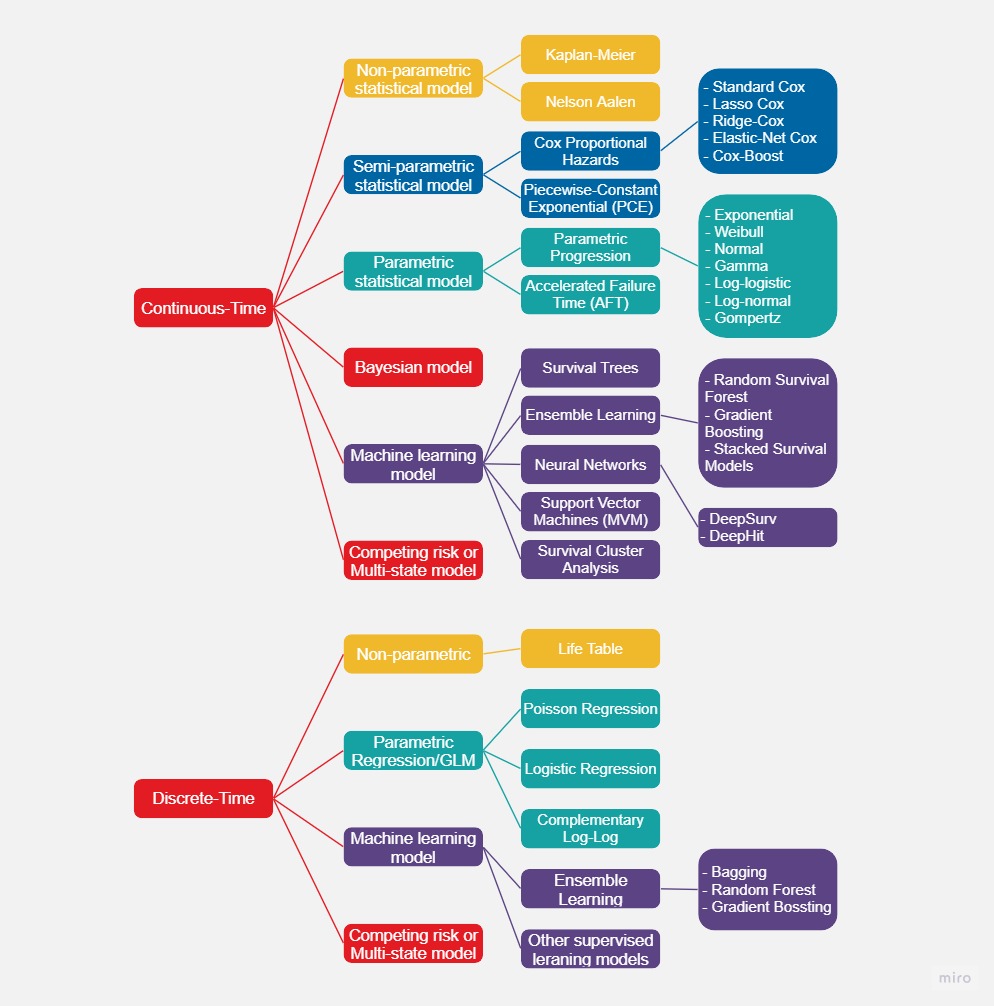
2. Machine learning models for survival analysis
In recent years, machine learning models have achieved success in many areas. This is due to built-in strengths that include higher prediction accuracy, ability to model non-linear relationships, and less dependence on distribution assumptions. Nevertheless, some machine learning algorithms bring notable weaknesses as well, such as difficulty in interpretation, sensitivity to hyperparameters, and a tendency to overfit. Dealing with censored data presents the biggest challenge for using machine learning in survival analysis.
A deeper understanding of survival analysis, and how machine learning can overcome the challenge of censored data, is required in order to effectively adapt it to mortality modeling.
The discussion below starts with regularization – a versatile machine learning technique applicable to many approaches, including GLM and classical survival models. The total range of machine learning models is vast; therefore, I look just at continuous-time models and deliberately exclude some notable discrete-time approaches, for instance support vector machines and random forest. Discrete-time supervised machine learning models are discussed in Modeling Discrete Time to Event Data (Tutz and Schmid, 2018), while extensions of GLM are discussed in Section 3.
2.1 Regularization
Regularization is a technique used to simplify a model and reduce overfitting by adding penalties or constraints to the model-fitting problem. The three main types of regularization are:
i. Ridge, also known as Tikhonov or L2 regularization, adds a penalty term based on the squared value of coefficients. It reduces the size of coefficients and deals with correlations between features simultaneously.
ii. Lasso (least absolute shrinkage and selection operator), also known as L1 regularization, adds a penalty term based on the absolute value of coefficients. In contrast to Ridge, Lasso can shrink coefficients to zero, which means it can perform automatic variable selection. Extensions of Lasso include Group Lasso, Fused Lasso, Adaptive Lasso, and Prior Lasso.
iii. Elastic net linearly combines the Ridge and Lasso penalty terms.
2.2 Cox models
Introducing regularization into Cox proportional hazard models provides us with a form of machine learning – the resulting models include Ridge-Cox (Verweji and Van Houwelingen, 1994), Lasso-Cox (Tibshirani, 1997), and Elastic Net-Cox (Simon et al., 2011).
The Cox-Boost method (Binder and Schumacher, 2008) incorporates gradient boosting machines in Cox models. It is useful on high-dimensional data and considers some mandatory variables explicitly in the model.
2.3 Survival tree
Survival trees are classification and regression trees (CART) specifically designed to handle censored data (Gordon and Olshen, 1985). The data is recursively partitioned based on a splitting criterion and objects with similar survival times are grouped together. This approach is easier to interpret and does not rely on distribution assumptions.
2.4 Random survival forest and other ensemble methods
In machine learning, ensemble learning is a method that takes a weighted vote from multiple models to obtain better predictive performance than could be obtained from any of the constituent models alone. Common types of ensembles include bagging, boosting, and stacking.
Bagging survival trees involves taking a number of bootstrap samples from the survival data, building a survival tree for each sample, and then averaging the tree nodes’ predictions (Hothorn et al., 2004).
Random survival forest is similar to bagging, but random forest uses only a random subset of the features for selection at each tree node. This helps reduce the correlation between trees and improves predictions. Random survival forest does not depend on distribution assumptions and can be used to avoid the proportional hazards constraint of a Cox model (Ishwaran et al., 2008).
Boosting combines a set of simple models into a weighted sum and is iteratively fitted to the residuals based on the gradient descent algorithm. Hothorn et al. (2006) proposed gradient boosting to account for censored data.
Stacking combines the output of multiple survival models and runs it through another model. Wey et al. (2015) proposed a framework of stacked survival models that combines parametric, semi-parametric and non-parametric survival models. This approach has performed well by adaptively balancing the strengths and weaknesses of individual survival models.
2.5 Artificial neural networks
Artificial neural networks (ANN) consist of layers of neurons interconnected as a network to solve optimization problems. The adjective ‘deep’ in deep learning refers to the use of multiple layers in the network. Neural networks and survival forests are examples of non-linear survival methods.
The initial adaptation of survival analysis to neural networks sought to generalize Cox with only one single hidden layer (Farragi and Simon, 1995). Katzman et al. (2018) later proposed DeepSurv, a deep feed-forward neural network generalizing the Cox proportional hazards model. It has the advantage of not requiring a priori selection of covariates, by learning them adaptively.
DeepHit is a deep neural network that learns the distribution of survival times directly (Lee et al., 2018). Unlike parametric approaches, it makes no assumption of the underlying stochastic processes and allows for the relationship between covariates and risk to change over time. DeepHit can be used for survival datasets with a single mortality risk as well as multiple competing risks.
3. Extensions and enhancements of GLM
GLM is a popular tool in survival analysis due to its versatility, interpretability, predictive power, and availability in many software packages. Section 1 demonstrated that GLM Poisson, Logistic and C-Log-Log models can perform survival analysis. However, GLMs elicit two common negative views: they are restricted by distribution assumption, and they do not account for non-linear relationships, which reduces predictive performance.
The first view is refutable because, as discussed in Section 1, a GLM is merely a device to derive the underlying survival model, so the model is not restricted by distribution assumptions of GLM.
The second issue can be mitigated using approaches such as these to extend or enhance GLM. Note that these are not restricted to survival analysis and can be applied to GLMs in general. Some practitioners would view these as ways to combine the advantages of GLMs (for instance, interpretability) with the power of machine learning:
- Generalized additive model (GAM): GAM is a GLM in which one or more of the predictors depends linearly on some smooth functions, which is useful to capture non-linear patterns. Examples of smooth functions are cubic splines and fractional polynomials. This approach allows much more flexible models.
- Generalized linear mixed model (GLMM): The GLMM extends the GLM by incorporating random effect terms. GLMMs are also referred to as frailty models (Tutz and Schmid, 2018).
- Regularization such as elastic net to handle multicollinearity and reduce overfitting.
- Automatic variable selection using Lasso or elastic net. This can help identify influential risk factors efficiently rather than using stepwise selection, especially when the number of possible predictors is large.
- Identification of predictive interaction terms with the help of machine learning, such as decision trees or random forest. If interpretability is important, it is preferable to keep the interaction terms relatively simple, rather than incorporating an influential yet hard-to-interpret ‘blackbox’ sub-model, such as a neural network, into a GLM.
- Dimension reduction, by using unsupervised machine learning techniques, if there is a very large number of variables relative to the number of observations.
4. Applications in mortality modeling
Tedesco et al. (2021) constructed machine learning models to predict all-cause mortality in a two- to seven-year time frame in a cohort of healthy older adults. The models were built on features including anthropometric variables, physical and lab examinations, questionnaires, and lifestyle factors, as well as wearable data. Random forest showed the best performance, followed by logistic regression, AdaBoost, and decision tree. Additional insights could be extracted to gain understanding on healthy aging and long-term care.
Using the MIMIC-III dataset on long-term mortality after cardiac surgery and the AUC metric, the researchers observed the order of model performance, from highest to lowest, to be AdaBoost, logistic regression, neural network, random forest, Naïve Bayes, XGBoost, bagged trees and gradient-boosting machine (Yu et al., 2022).
The OpenSAFELY paper (Williamson, 2020) applied the multivariable Cox model to analyze data from 17 million patients in England and subsequently identified a range of risk factors for Covid-19 mortality This was instrumental in helping to identify high-risk population subgroups, as Dan Ryan describes elsewhere in this Bulletin. Later that year, RGA (Ng et al., 2020) published a paper that cross-compared an all-cause mortality model with OpenSAFELY’s Covid-19 model in a parallel and multivariable way. This revealed insights on excess mortality risk from certain factors, which were useful to actuaries and underwriters. Six months later, the OpenSAFELY team published another paper (Bhaskaran et al., 2021) analyzing Covid-19 and non-Covid-19 mortality odds ratios, by using logistic regression. The team produced results that were very consistent with RGA’s.
Conclusion
The goal of mortality modeling is to predict and understand mortality and longevity. This article provides a survey and taxonomy of mortality modeling under the survival analysis framework, structured by continuous-time and discrete-time, as well as statistical methods and machine learning. The choice of model depends on the nature of the data and the purpose – whether it is solely about predictive accuracy or if interpretability is important.
Due to the increasing availability of data, technology and development in survival analysis and machine learning, financial services providers, such as insurers and pension funds, can leverage advances in these areas to provide financial protection more effectively to more people.
Reprinted with permission of The Institute and Faculty of Actuaries.